Fix a family of forbidden patterns on a transitive graph, i.e. some colorings of some finite subgraphs. Consider an iid coloring on the full graph (or a finite subset) conditioned to avoid all the forbidden patterns. What does a typical configuration look like, and what statistical properties does it have? This model originated in ergodic theory and symbolic dynamics, and lies at the intersection of probability, combinatorics, dynamics, and statistical physics. Many interesting questions arise already in the one dimensional setting. For example: consider bi-infinite binary words, and forbid a single binary pattern. The entropy of the resulting shift space (i.e. the exponential growth rate of the number of allowable words) is described by a simple combinatorial statistic, the auto-correlation polynomial of the forbidden word. In higher dimensions, computing the entropy or establishing mixing properties is much more challenging; and in the non-amenable setting, a nice notion of entropy is still not known. Another natural object is the asymptotic density of 1s, or of another fixed (allowable) pattern. Is there a similar combinatorial statistic that describes these densities?

In the 1980s physicists Per Bak, Chao Tang and Kurt Wiesenfeld coined and popularized the idea of self organized criticality (SOC), a phenomenon they observed in real-world systems like avalanches and forest fires. In these systems, energy slowly builds up over time, and is released in shocks with sizes that follow a statistical power law. They proposed a number of simple but mathematically challenging models to study SOC, including the abelian sandpile model, a precursor to activated random walk (ARW). Deepak Dhar later proved that the sandpile has a certain abelian property, which is shared by activated random walk. 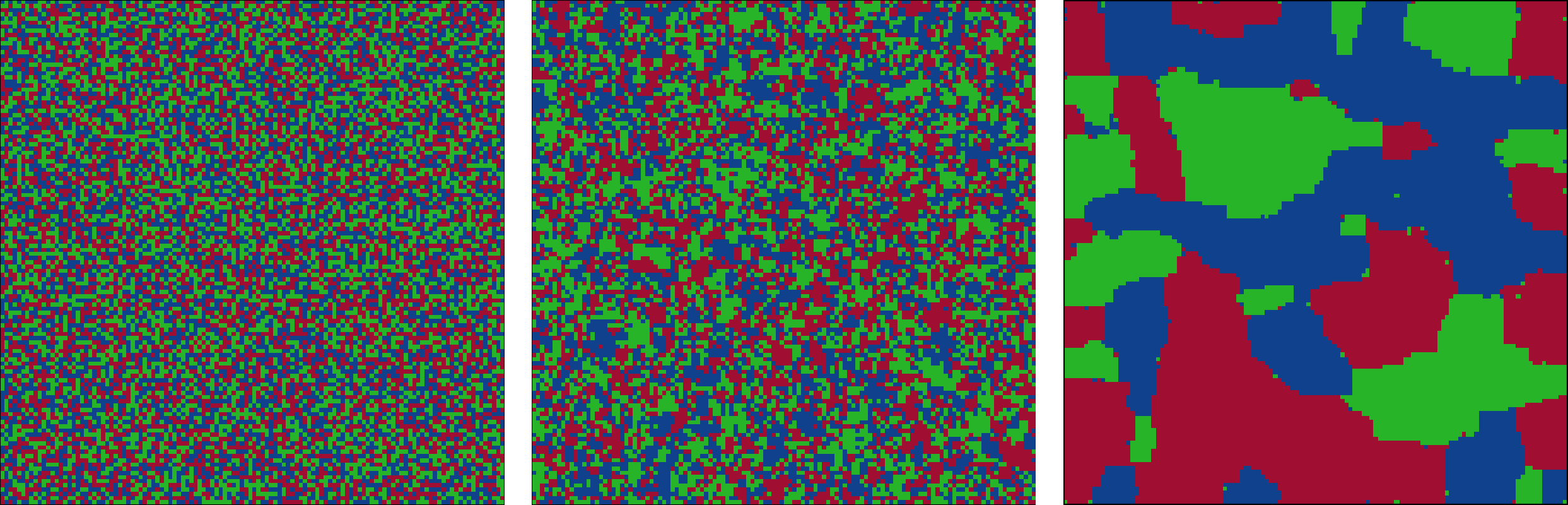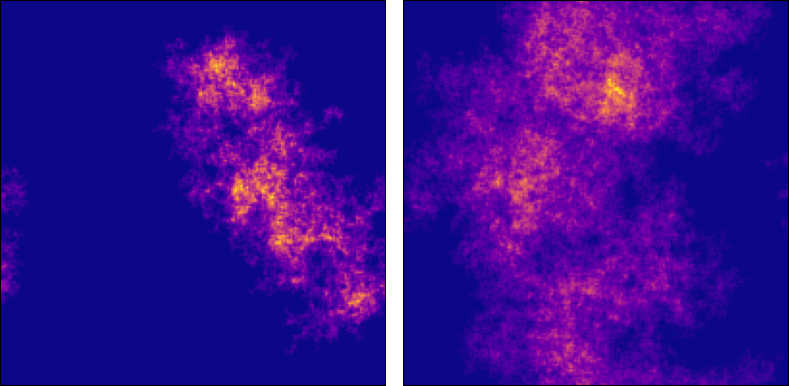Simulations suggest that ARW has a critical limiting state that exhibits SOC in a robust way, with little dependence on the exact setup of the model. Research on ARW has recently gained traction, and many results on the critical density are now available. Still, we lack a mathematical description of exactly how SOC arises for ARW. While the two-dimensional case is of particular practical interest, ARW in one dimension, on a tree, or in the mean field (on the complete graph) are more tractable, and are not yet fully solved.

I am often drawn to questions about random combinatorial objects: markov chains, fragmentation/coagulation processes, interacting particle systems, renewal processes, random number theory. Proving limit theorems, describing stationary configurations or evolutions, or studying mean field behavior of these systems, to name a few objectives, often leads to cutting edge ideas and unsolved problems.

Run a random growth model or diffusion on a graph up to a fixed time. Given only a snapshot of the set of sites visited by the process, what information can be determined about the process? Can you guess the starting point, the ending point, most visited point, or the distribution of the process? These kinds of questions arise in applied computer science, for example in infection spread through a social network. Giving a precise answer for simple random walk in \(\mathbb{Z}^d\) is already a difficult problem.

Consider independent site percolation on a finite graph, like a subset of \(\mathbb{Z}^d\) or the hexagonal lattice. How many open clusters are there? For example, what is the expected number of clusters? For lattices, it is easy to see that the number of clusters is on the same order as the volume of the set you percolate. Can one establish a law of large numbers for the cluster count, and compute the limiting constant? The A5 problem from the 2004 Putnam exam asked to prove a lower bound on this constant. But exactly determining it is a difficult problem.

Consider an iid sequence of random sets, or a Poisson point process of hyperplanes or sets in a metric space. One can ask many natural questions related to the coverage of such a family of sets: what is their union? What is the distribution of the random field counting how many times each point is covered by the union? If the sequence is confined to a compact set, what is the intersection of the sets? A canonical limit object, called the Crofton cell, often arises in connection with these questions, appearing (for example) as the scaling limit of the region containing the origin in a standard hyperplane tesselation of \(\mathbb{R}^d\).